Circle Texturing
Rastering is a well known topic from the print media. Originally it was used for shading one-color prints to create light and shadow effects. Wood engraving was one prominent technique, used by Doré, Escher, and others. Nowadays rastering is used prominently on microscopic level in multi-color printing.
Modern graphics and design inherit from these fields. Tiresome manual work with surfaces has been automated to a large extent, and complete mathematical models open up even more possibilities for designers.
Which brings me to the topic of generative art.
Circle form is very easy to model and constrain mathematically, so when I decided to investigate texturing, it felt natural to start with circles.

In this work, I restrict to one color fills, because they are like basic building blocks that are easy to combine, once that they are first well defined. The first image shows just a line of solid greyscale fills, for reference.
Source code for all the images to follow is found here.

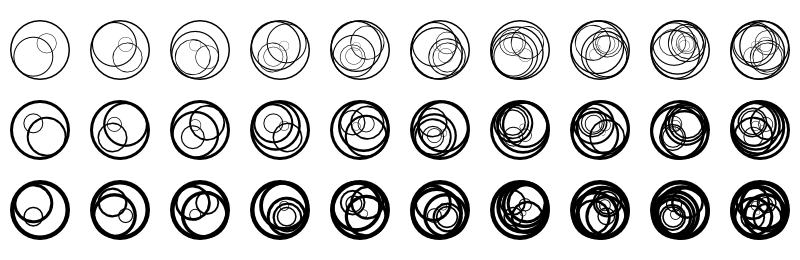
Cocentric subcircles may be the most simple method for texturing a circle.
Yet there are many possibilities for variation already. I increase the number of circles from left to right, and the width of the stroke from top towards bottom.

Another very simple method is to use regularly placed sectors fro marking the circle. Here I vary the number of sectors and sector-to-empty ratio.

Probably next up in simplicity is a spiral fill. If visual variation is desired, it can be created by drawing with straight line segments. When they are short enough, the spirals will look ordinary, but if they are very long, some polygon-like patterns start to emerge.
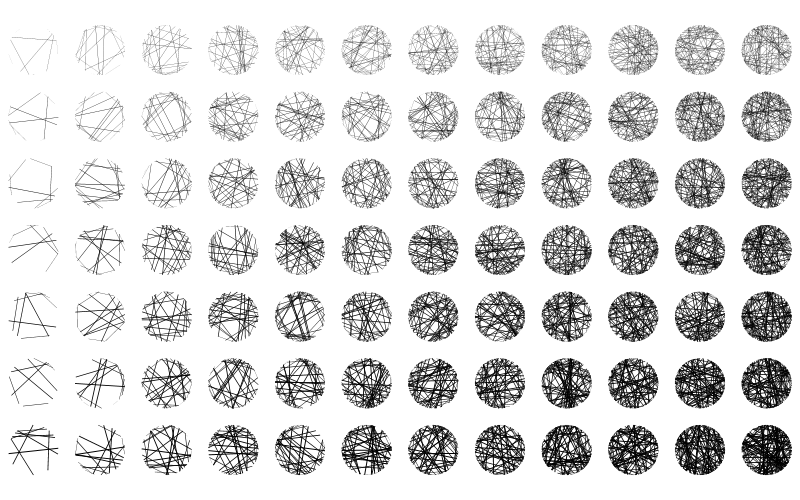
Random lines that connect two points on the circle perimeter produce very pleasing results. It feels rewarding that the apparently random lines add up to perfect circles in such complete way.
Each line is completely defined by the circle and at the same time completely random.
Relaxing one of the line ends so that it is allowed to lie anywhere within the circle makes the circles immediately more messy. It also creates a bias towards the circle center, since more lines will probably meet there than in any other single point within the circle.

Line endpoints can, on the other hand, be constrained to some fixed frequency on the circle perimeter.
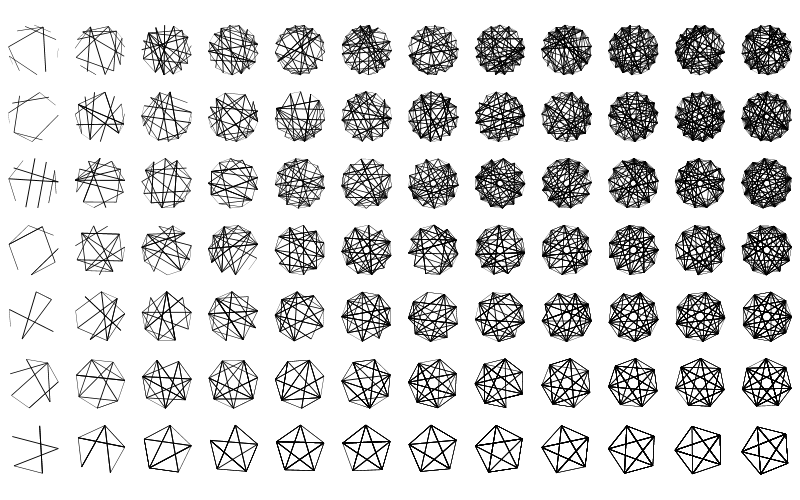
Perceived randomness is decreased, but it still looks gratifying to see the structured forms complete themselves within the circle perimeter.
Frequency decreases here from top to bottom, and the number of lines increases from left to right.

Vertical lines can fill the circle form too.
The visual form becomes a little bit more interesting, when an occassional slant is introduced.

A horizontal one can be obtained simply by rotating the vertical fill by 90 degrees.
Along the same lines, a line bouncing back and forth between two sides of the perimeter creates a completely new, water or mistlike effect.

A very regular hatch pattern, then, can be created from two perpendicular line fills.
Notice the two variants, one created from simple perpendicular lines and the other created from two sets of pounding lines.
The latter one has a modern denim-like feel, whereas the prior one looks markedly olden, like 1920s printed newspaper comics.


In these examples, the number of lines and stroke width are varied. Base rotation is varied in the first one.
By overlaying three or even four fills in different angles, we receive even more patterns, but I didn’t find them as interesting visually as the two-based alternatives.
Turning to another topic, circle packing, yay!

I created my own quick algorithm for this picture. It receives as parameter the number of cocentric rings on which to place circles, and a ratio value [0..1] for empty space vs. subcircle radius.
This was fairly fast and simple, and circles seemed to cluster the center easily, and create a “black spot” there. I added a penalty that disables some tightly placed subcircles. I also break regularity here slightly by placing circles on a ring in a wavy manner. Results are quite pleasing and timeless to my eye.
Any shape that fits inside a circle can be used for the packing, so I tried with some bezier shapes, as well as with non-filled circles of varying stroke..



These are relatively regular and the eye perceives them as containing some order. In contrast, circle packing with a simple contextual model (octree in my case), can produce fills with a more random feel, where anyway the subshapes don’t overlap.


In order to keep it more interesting, I introduce some order in the way to where random sub-circles can be placed and where not.
Without this kind of adjustment the blots appear more random.

This can be further enhanced to produce a kind of Rorschach ink blot effect, if the restriction is lifted that circles can’t overlap.
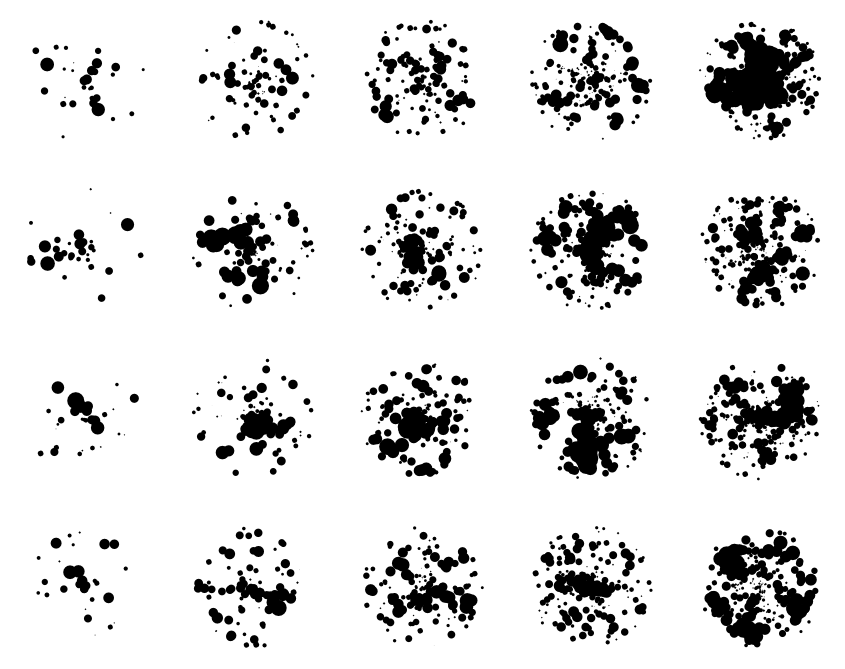

I use a Worley type noise source to create some structure here, determining sub-circle size based on worley noise 1st or 2nd order distance.
Now what has been outlined here were all relatively simple and easy ways to fill the circle. What I omitted due to laziness, mostly, were dashed filles and more organic circle packings, as well as more intricately varying oscillator based models which I have been working on lately.
But now for the combinations. What components are used in following “combo fills” is left as an exercise for the reader :)